NCERT Solutions for Class 10 Maths New Updated 2021-22 Session – Free PDF Download
We provide Chapter wise NCERT Solutions for Class 10 Maths from Chapters 1 to 15 that are based on latest CBSE syllabus and latest CBSE Exam pattern. These NCERT Solutions are curated by many expert teacher to help students in their board exam preparations as well as other competitive exams. Students who are searching for the chapter wise NCERT Solutions for Class 10 Maths can download from here. Student can also check the Important Question with solution for class 9 to class 12.
Also Check – 5 Best Laptop under 30000 in India
Mathematic are scoring subject in class 10 you can easily get very good marks in your board exam and NCERT solutions class 10 maths are extremely helpful for students preparing for the 10th board examinations. You can download the chapter-wise solution of class 10 math right below.
Chapter-wise NCERT solution for class 10 Maths
- Chapter 1 Real Numbers
- Chapter 2 Polynomials
- Chapter 3 Pair of Linear Equations in Two Variables
- Chapter 4 Quadratic Equations
- Chapter 5 Arithmetic Progressions
- Chapter 6 Triangles
- Chapter 7 Coordinate Geometry
- Chapter 8 Introduction to Trigonometry
- Chapter 9 Some Applications of Trigonometry
- Chapter 10 Circles
- Chapter 11 Constructions
- Chapter 12 Areas Related to Circles
- Chapter 13 Surface Areas and Volumes
- Chapter 14 Statistics
- Chapter 15 Probability
Due to the recent pandemic situation, CBSE divided class 10 syllabus in two part in Term 1 and Term 2. 1st term syllabus cover the chapter Number System, Algebra, Coordinate Geometry, Geometry, Trigonometry, Mensuration and Statistics and Probability. You can find the table and marking system of class 10 term 1 exam.
CBSE Term 1 Syllabus & Marking Scheme for class 10 Maths 2021-22
| Units | Unit Name | Marks |
| I | Number Systems | 06 |
| II | Algebra | 10 |
| III | Coordinate Geometry | 06 |
| IV | Geometry | 06 |
| V | Trigonometry | 05 |
| VI | Mensuration | 04 |
| VII | Statistics and Probability | 03 |
| Total | 40 | |
| Internal Assessment | 10 | |
| Grand Total | 50 |
Class 10 Mathematic Term 2 syllabus cover the topic Algebra (Cont.), Geometry (Cont.), Trigonometry (Cont.), Mensuration (Cont.), and Statistics and Probability (Cont.). You can find the table and marking system of class 10 term 1 exam.
CBSE Term 2 Syllabus & Marking Scheme for class 10 Maths 2021-22
| Units | Unit Name | Marks |
| I | Algebra (Cont.) | 10 |
| II | Geometry (Cont.) | 09 |
| III | Trigonometry (Cont.) | 07 |
| IV | Mensuration (Cont.) | 06 |
| V | Statistics and Probability (Cont.) | 08 |
| Total | 40 | |
| Internal Assessment | 10 | |
| Grand Total | 50 |
NCERT Solutions for Class 10 Maths Chapter 1- Real Numbers
In the 1st Chapter of Class students will learn about real numbers and irrational numbers. In CBSE Class 10 Maths Chapter 1 explains Euclid’s Division Lemma, HCF, LCM, Divisibility of integers, rational number, irrational number and decimal expansion of rational numbers with the help of theorem.
Real Number is one of the important topics in Maths and it has a weightage of 6 marks (1×1 Marks, 2×1 Marks and 3×1 marks) in Class 10 (Unit – Number Systems) Maths first term exams. The average number of questions asked from this chapter is usually 3.
- One out of three questions in part A (1 marks).
- One out of three questions in part B (2 marks).
- One out of three questions in part C (3 marks).
NCERT Solutions for Class 10 Maths Chapter 2- Polynomials
There are a total of 4 Exercises including an optional Exercise in the 2nd chapter of class 10 Maths. In this chapter we learn about Properties zeros and coefficient, long division of polynomials, finding a quadratic polynomial, relationship between 0’s and coefficients of a polynomial and lastly division of polynomials.
NCERT Solutions for Class 10 Maths Chapter 3 – Pair of Linear Equations in Two Variables
Chapter 3 – Pair of Linear Equations Class 10 has total of seven exercises and that consists of 55 questions and it weightage of 11 marks in the examinations. It describes what a linear equation in two variables is and how to solve the problems of linear equations in two variables.
Important Formulas –
The general form for a pair of linear equations in two variables x and y is
a1 x + b1 y + c1 = 0
and a2 x + b2 y + c2 = 0,
where a1, b1, c1, a2, b2, c2 are all real numbers and a12 + b12 ≠ 0, a22 + b22 ≠ 0.
NCERT solution for class 10 Maths Chapter 4 – Quadratic Equations Exercise 4
Class 10 Maths Chapter 4 Quadratic Equations chapter contain total 7 exercise and it covered the topic in-depth explanation, method of solving the quadratic equation through the factorisation method, completing the square method finding the roots of the equation, and splitting the middle term.
NCERT Solutions for Class 10 Maths Chapter 5 – Arithmetic Progressions
Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5 chapter contain total 4 exercise and it covered the topic form of AP, finding the first term and difference of an AP, finding the nth term of an AP, sum of first n terms of an AP.
Important Formulas:
- nth term of AP: an = a + (n – 1) d
- Sum of n terms: S = n/2[2a + (n – 1) d]
NCERT Solutions for Class 10 Maths Chapter 6 Triangles Exercise 6
Class 10 Maths Chapter 6 Triangle has total six exercises and it exercise consists total 64 questions. All the based on given theorems.
Important Theorems –
- Theorem 6.1: If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
- Theorem 6.2: If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
- Theorem 6.3: If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar.
- Theorem 6.4: If in two triangles, sides of one triangle are proportional to (i.e., in the same ratio of ) the sides of the other triangle, then their corresponding angles are equal and hence the two triangles are similar.
- Theorem 6.5: If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar.
- Theorem 6.6: The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
- Theorem 6.7: If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse, then triangles on both sides of the perpendicular are similar to the whole triangle and to each other.
- Theorem 6.8: In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
- Theorem 6.9: In a triangle, if square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Exercise 7
Class 10 Maths Chapter 7 Coordinate Geometry Exercise 7 chapter contain total 4 exercise that has 33 questions and it covered the topic finding polynomials, Properties zeros and coefficient, area of the triangle formed by three given points. , long division of polynomials, find coordinates of the point which divides a line segment, finding a quadratic polynomial.
Important formula
Distance Formula
The distance between any two points
P(x1, y1) and Q(x2, y2) in the plane is given by,![]()
Also the distance of the point P(x1, y1) from the origin is![]()
Section Formula
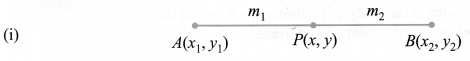
The coordinates of the point P(x, y) which divides the line segment joining the points A(x1, y1) and B(x2, y2) internally in the ratio m1 : m2 i.e., 𝑃𝐴𝑃𝐵=𝑚1𝑚2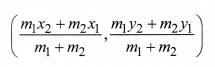
The coordinates of the point P(x, y) which divides the line segment joining the points A(x1, y1) and B(x2, y2) externally in the ratio, m1 : m2 i.e., 𝑃𝐴𝑃𝐵=𝑚1𝑚2 are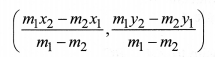
(iii) If the ratio in which P divides AB is K : 1, then the coordinates of the point P will be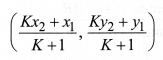
Mid-Point Formula
The coordinates of the mid point P of the line segment joining the points A(x1, y1) and B(x2, y2) is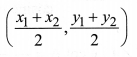
Area of a Triangle
The area of ∆ABC formed by the vertices A(x1, y1), B(x2, y2) is given by![]()
Note:
(i) Area of triangle = 12 × base × Altitude
(ii) Area of polygon can be calculated by dividing it into the triangular region.
(iii) If three points are collinear then area of the triangle formed by them is zero.
NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Exercise 8
Class 10 Maths Chapter 8 Introduction to Trigonometry Exercise 8 contain total 4 exercise that has 27 questions and it covered the topic trigonometric ratios of the angles, trigonometric ratios for angles of 00 and 900 , trigonometric ratios of complementary angles.
Important Formula
Trigonometric Ratios of Complementary Angles
sin (90° – A) = cos A,
cos (90° – A) = sin A,
tan (90° – A) = cot A,
cot (90° – A) = tan A,
sec (90° – A) = cosec A,
cosec (90° – A) = sec A
sin2 A + cos2 A = 1,
sec2 A – tan2 A = 1 for 0° ≤ A < 90°,
cosec2 A = 1 + cot2 A for 0° < A ≤ 90°
Trigonometry Table
| Angle | 0° | 30° | 45° | 60° | 90° |
| Sinθ | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| Cosθ | 1 | √3/2 | 1/√2 | ½ | 0 |
| Tanθ | 0 | 1/√3 | 1 | √3 | Not defined |
| Cotθ | Not defined | √3 | 1 | 1/√3 | 0 |
| Secθ | 1 | 2/√3 | √2 | 2 | Not defined |
| Cosecθ | Not defined | 2 | √2 | 2/√3 | 1 |
Trigonometric Ratios
Trigonometric ratios of an acute angle in a right triangle express the relationship between the angle and the length of its sides.
Let ∆ABC be a triangle right angled at B. Then the trigonometric ratios of the angle A in right ∆ABC are defined as follows: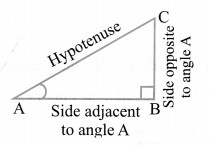

NCERT Solutions for Class 10 Maths Chapter 9 Some Applications of Trigonometry Exercise 9
Class 10 Maths Chapter 9 Some Applications of Trigonometry Exercise 9 contain only 1 exercise that has 16 questions and it covered the topic how find the heights and distances of different objects using trigonometry.
Important Point-
Line of Sight and Angle of Elevation
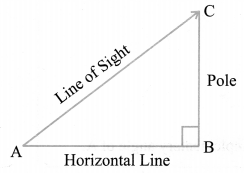
In the above figure, the line AC drawn from the eye of an observer at A to the top of the pole ‘C’ is called the line of sight. The observer is looking at the top of the pole. The angle BAC, so formed by the line of sight with the horizontal, is called the angle of elevation of the top of the pole from the eye of an observer.
Angle of Depression
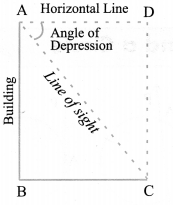
In the above figure, the line AC, is the line of sight as the observer is looking downwards from the top of the building at A towards the object at C. Here angle DAC, so formed by the line of sight with the horizontal, when the observer is lowering his/her head is called Angle of depression.
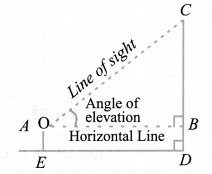
From the above figure, if we want to find the height CD of the pole without actually measuring it, we need the following information:
(i) Distance ED of the observer from the pole.
(ii) the angle of elevation ∠BAC, of the top of the pole.
(iii) the height AE of the observer if it is considerable.
Assuming that the above three conditions are known we can determine the height of the pole in the following way.
In the figure, CD = CB + BD. Here, BD = AE, which is the height of the observer.
To find BC, we will use trigonometric ratios of ∠BAC or ∠A.
In ∆ABC, the side BC is the opposite side to the known ∠A. Now we use either tan A or cot A, as these trigonometric ratios involve AB and BC to find BC.
Therefore, tan A = 𝐵𝐶/𝐴𝐵 or cot A = 𝐴𝐵/𝐵𝐶, which on solving would give us BC. By adding AE to BC, you will get the height of the pole.
FAQs
There are total 15 exercises in Class 10 Maths.
I feel that trigonometry is the most difficult chapter of class 10th maths.
Make Notes for Formulas, Theorems and Methods using NCERT book.
Solve the given NCERT book Example.
Practicing the sample and previous year questions papers.
Cover all Syllabus within time.
Revise the NCERT Books.
Find out your weak points.
relations and functions and linear programming are simple.








