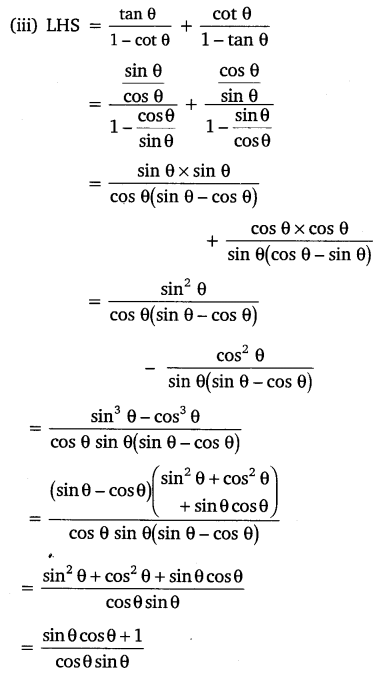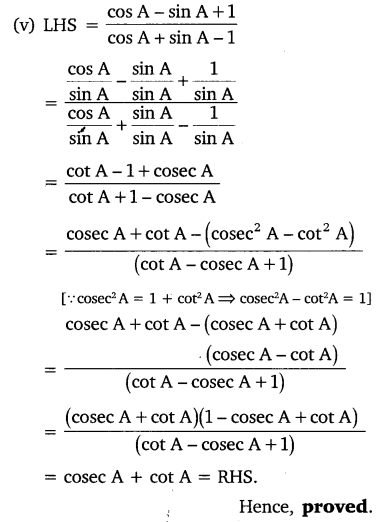NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Exercise 8
NCERT Solutions For Class 10 Maths Chapter 8 Introduction to Trigonometry Exercise 8 are prepared by specialised experienced mathematic teacher. Maths are most important subject of board and with the help of this chapter-wise NCERT solution and little practices you can get very good marks in your respective board exam. It also help to build a foundation for topics that will be covered in the upcoming 11th and 12th. Student can also check the Important Question with solution for class 9 to class 12.
Also Check – Best laptop under 30000 for student
Class 10 Maths Chapter 8 Introduction to Trigonometry Exercise 8 contain total 4 exercise that has 27 questions and it covered the topic trigonometric ratios of the angles, trigonometric ratios for angles of 00 and 900 , trigonometric ratios of complementary angles. Check Previous chapter – NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry.
Important Formula
Trigonometric Ratios of Complementary Angles
sin (90° – A) = cos A,
cos (90° – A) = sin A,
tan (90° – A) = cot A,
cot (90° – A) = tan A,
sec (90° – A) = cosec A,
cosec (90° – A) = sec A
sin2 A + cos2 A = 1,
sec2 A – tan2 A = 1 for 0° ≤ A < 90°,
cosec2 A = 1 + cot2 A for 0° < A ≤ 90°
Trigonometry Table
| Angle | 0° | 30° | 45° | 60° | 90° |
| Sinθ | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| Cosθ | 1 | √3/2 | 1/√2 | ½ | 0 |
| Tanθ | 0 | 1/√3 | 1 | √3 | Not defined |
| Cotθ | Not defined | √3 | 1 | 1/√3 | 0 |
| Secθ | 1 | 2/√3 | √2 | 2 | Not defined |
| Cosecθ | Not defined | 2 | √2 | 2/√3 | 1 |
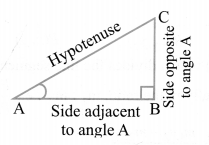
Trigonometric Ratios
Trigonometric ratios of an acute angle in a right triangle express the relationship between the angle and the length of its sides.
Let ∆ABC be a triangle right angled at B. Then the trigonometric ratios of the angle A in right ∆ABC are defined as follows:

Exercise 8.1
Question 1.
In ∆ABC right angled at B, AB = 24 cm, BC = 7 cm. Determine:
(i) sin A, cos A
(ii) sin C, cos C
Solution:
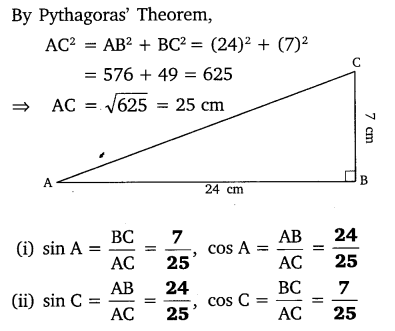
Question 2.
In given figure, find tan P – cot R.
Solution:

Question 3.
If sin A = 3/4, Calculate cos A and tan A
Solution:
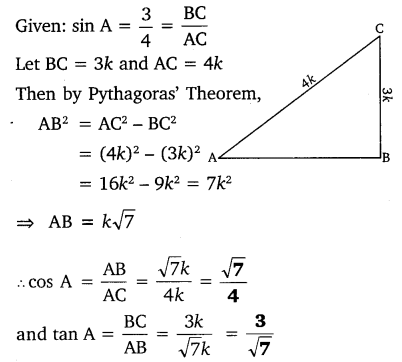
Question 4.
Given 15 cot A = 8, find sin A and sec A.
Solution:

Question 5.
Given sec θ = 13/12 Calculate all other trigonometric ratios
Solution:

Question 6.
If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Solution:

Question 7.
If cot θ = 78, evaluate:
(i) (1+𝑠𝑖𝑛𝜃)(1−𝑠𝑖𝑛𝜃)(1+𝑐𝑜𝑠𝜃)(1−𝑐𝑜𝑠𝜃)
(ii) cot²θ
Solution:

Question 8.
If 3 cot A = 4, check whether 1−𝑡𝑎𝑛2𝐴1+𝑡𝑎𝑛2𝐴 = cos² A – sin² A or not.
Solution:

Question 9.
In triangle ABC, right angled at B, if tan A = 1√3, find the value of:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Solution:

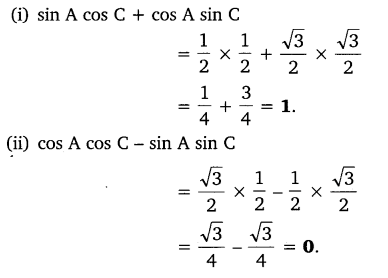
Question 10.
In ΔPQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Solution:

Question 11.
State whether the following statements are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = 125 for some value of angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ = 43 for some angle.
Solution:

Exercise 8.2
1. Evaluate the following:
(i) sin 60° cos 30° + sin 30° cos 60°
(ii) 2 tan2 45° + cos2 30° – sin2 60

Solution:
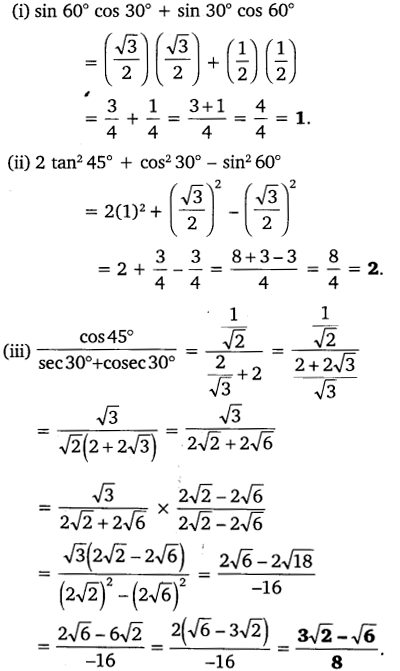
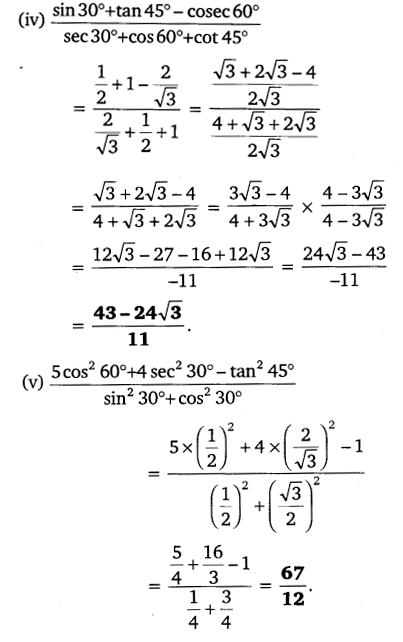
Question 2.
Choose the correct option and justify your choice:
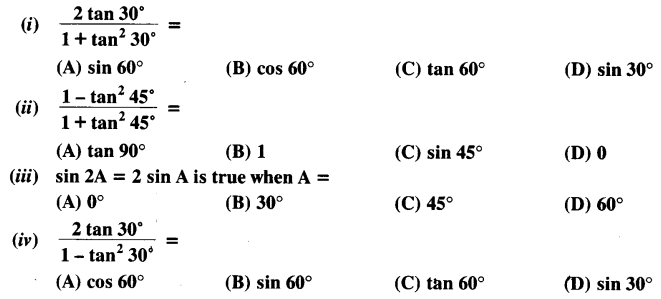
Solution:

Question 3.
If tan (A + B) = √3 and tan (A – B) = 1√3; 0° < A + B ≤ 90°; A > B, find A and B.
Solution:
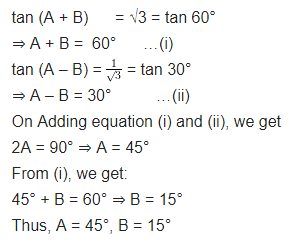
Question 4.
State whether the following statements are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B.
(ii) The value of sin θ increases as θ increases.
(iii) The value of cos θ increases as θ increases.
(iv) sin θ = cos θ for all values of θ.
(v) cot A is not defined for A = 0°.
Solution:
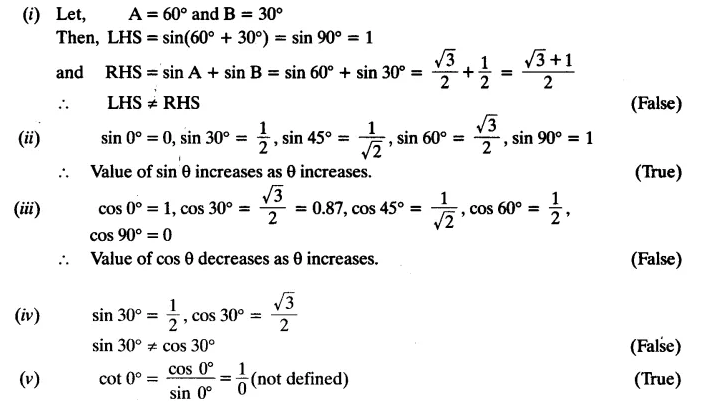
Exercise 8.3
Question 1.
Evaluate:
![]()
Solution:
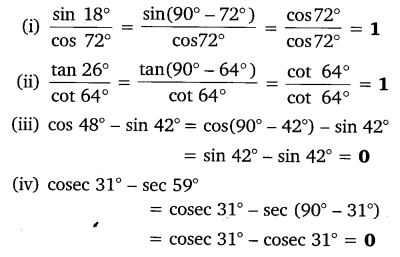
Question 2.
(i) tan 48° tan 23° tan 42° tan 67° = 1
(ii) cos 38° cos 52° – sin 38° sin 52° = 0
Solution:

Question 3.
If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A.
Solution:
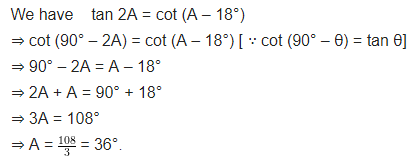
Question 4.
If tan A = cot B, prove that A + B = 90°.
Solution:
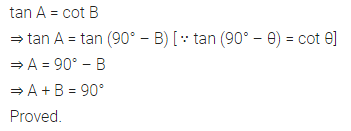
Question 5.
If sec 4A = cosec (A – 20°), where 4A is an acute angle, find the value of A.
Solution:
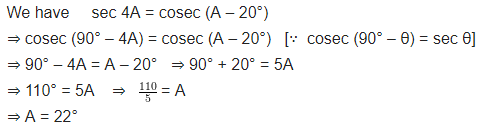
Question 6.
If A, B and C are interior angles of a triangle ABC, then show that: sin (𝐵+𝐶2) = cos 𝐴2
Solution:
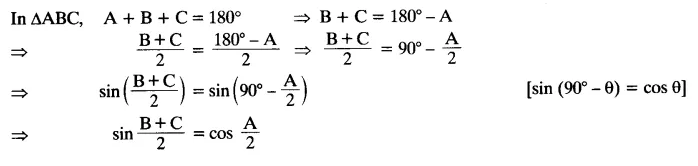
Question 7.
Express sin 61° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Solution:
![]()
Exercise 8.4
Question 1.
Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Solution:

Question 2.
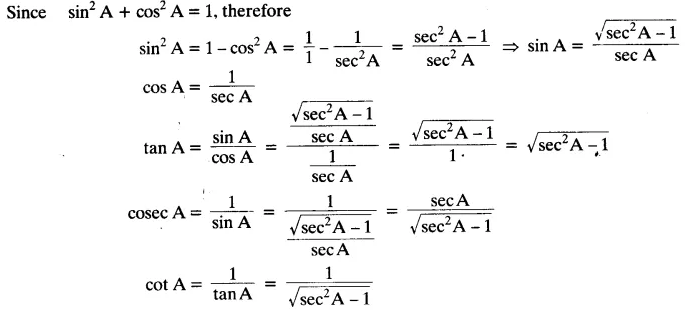
Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution:
Question 3.
Evaluate:
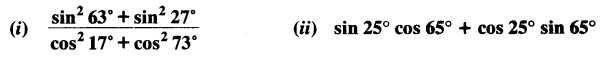
Solution:
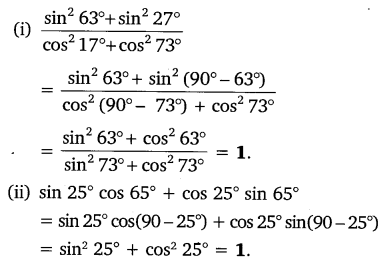
Question 4.
Choose the correct option. Justify your choice.
(i) 9 sec2A – 9 tan2A =
(A) 1 (B) 9 (C) 8 (D) 0
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ)
(A) 0 (B) 1 (C) 2 (D) – 1
(iii) (sec A + tan A) (1 – sin A) =
(A) sec A (B) sin A (C) cosec A (D) cos A
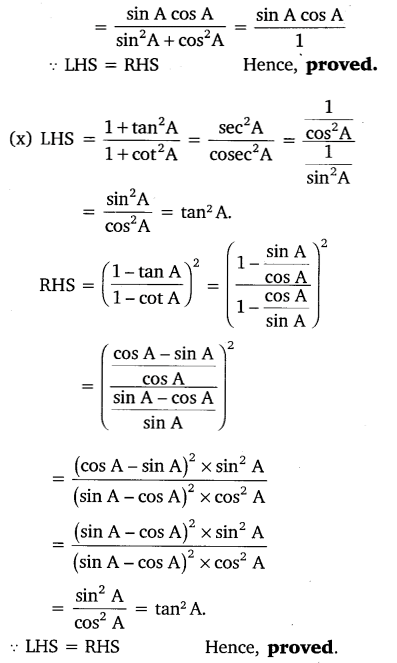
(iv) 1+tan2A/1+cot2A =
(A) sec2 A (B) -1 (C) cot2A (D) tan2A
Solution:

Question 5.
Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
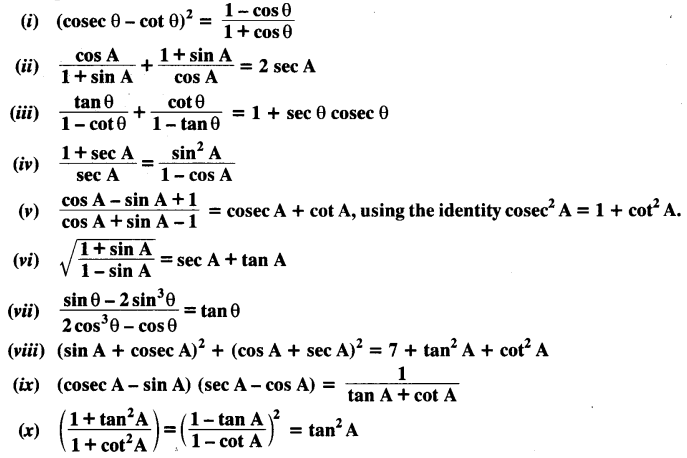
Solution: