NCERT Solutions for Class 10 Maths Chapter 11 Constructions

NCERT Solutions for Class 10 Maths Chapter 11 Constructions Exercise 11

NCERT Solutions For Class 10 Maths Chapter 11 Constructions Exercise 11 are prepared by specialised experienced mathematic teacher. Maths are most important subject of board and with the help of this chapter-wise NCERT solution and little practices you can get very good marks in your respective board exam. It also help students to build a foundation of upcoming class 11th and 12th. Student can also check the Important Question with solution for class 9 to class 12.

Also Check – 5 Best Laptop under 30000 in India 2022

Class 10 Maths Chapter 9 Some Applications of Trigonometry Exercise 9 contain only 1 exercise that has 16 questions and it covered the topic how find the heights and distances of different objects using trigonometry. Check Previous chapter – NCERT Solutions for Class 10 Maths Chapter 10 Circles

Exercise 11.1

Question 1.
Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts.
Solution:

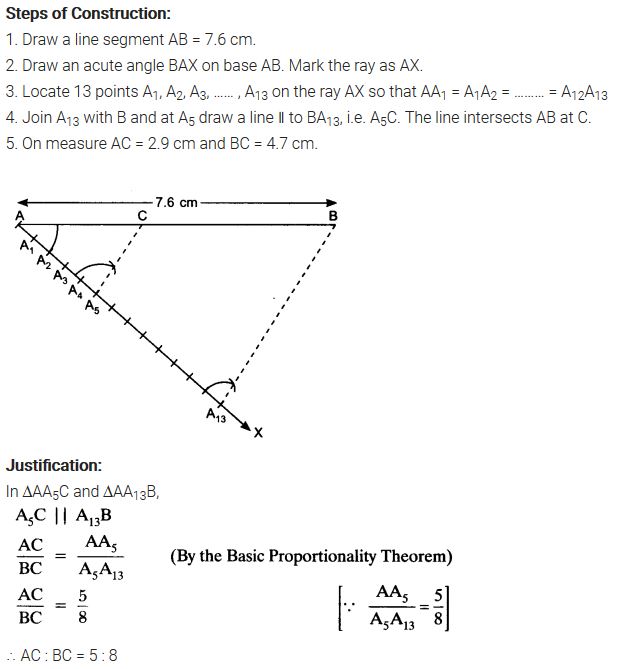
Question 2.
Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are 23 of the corresponding sides of the first triangle.
Solution:

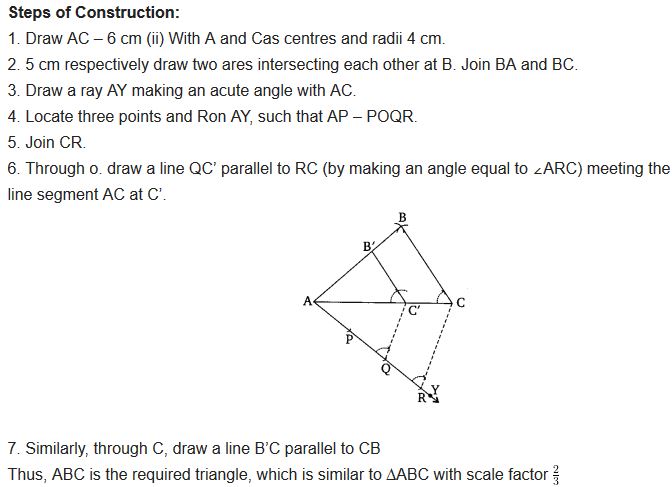
Question 3.
Construct a triangle with sides 5 cm, 6 cm, and 7 cm and then another triangle whose sides are 75 of the corresponding sides of the first triangle.
Solution:

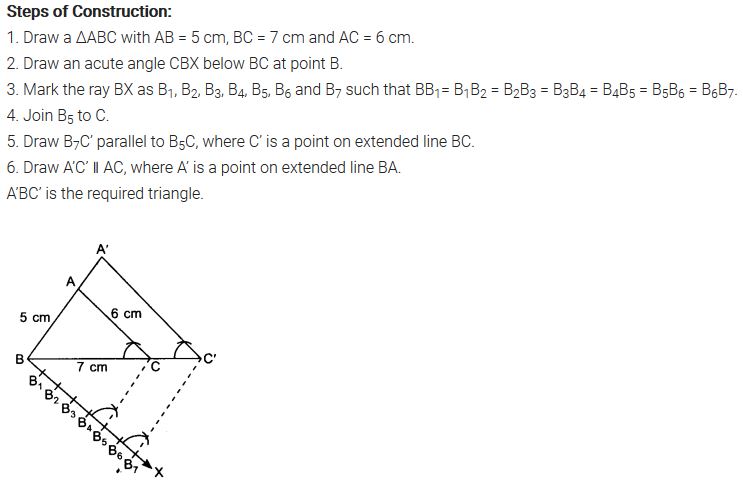
Question 4.
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 112 times the corresponding sides of the isosceles triangle.
Solution:

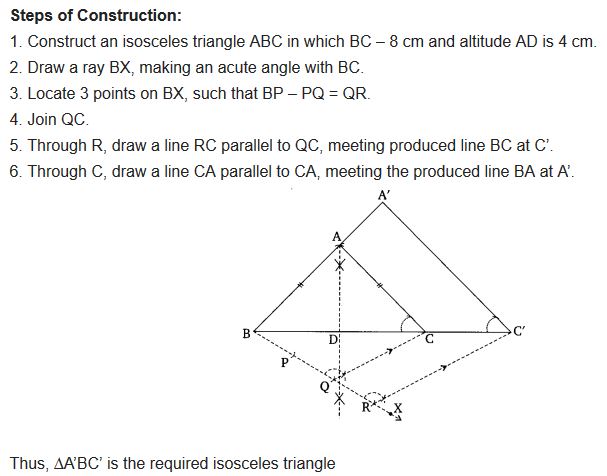
Question 5.
Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides are 34 of the corresponding sides of the triangle ABC.
Solution:

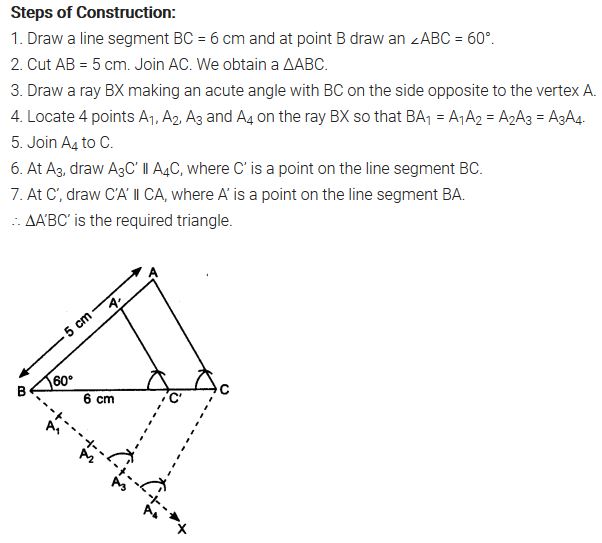
Question 6.
Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then, construct a triangle whose sides are 43times the corresponding sides of ∆ABC.
Solution:

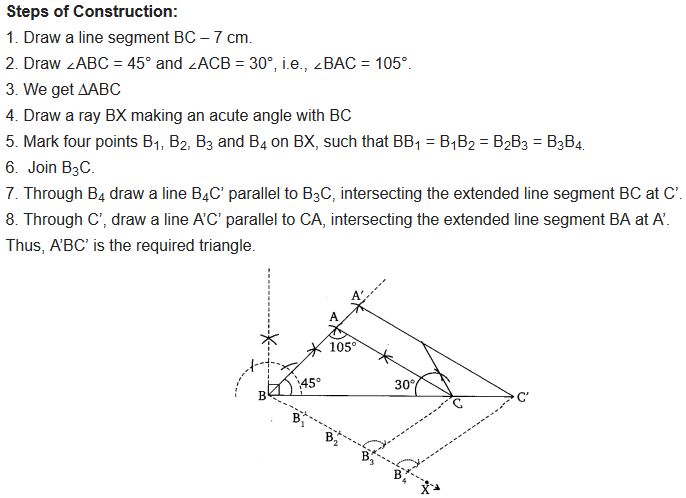
Question 7.
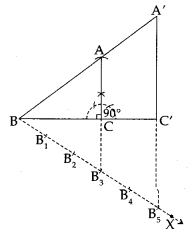
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are 5/3𝐹 times the corresponding sides of the given triangle.
Solution:
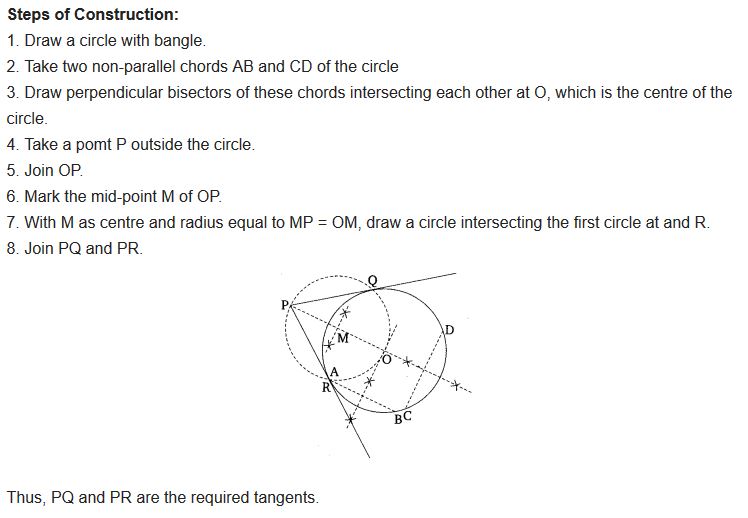
Steps of Construction:
1. Construct a ∆ABC, such that BC = 4 cm, CA = 3 cm and ∠BCA = 90°
2. Draw a ray BX making an acute angle with BC.
3. Mark five points B₁, B₂, B₃, B₄ and B₅ on BX, such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B_5.
4. Join B₃C.
5. Through B₅, draw B₅C’ parallel to B₃C intersecting BC produced at C’.
6. Through C’, draw C’A’ parallel to CA intersecting AB produced at A’.
Thus, ∆A’BC’ is the required right triangle.

Justification:

Exercise 11.2

Question 1.
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Solution:

Question 2.
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Solution:

Question 3.
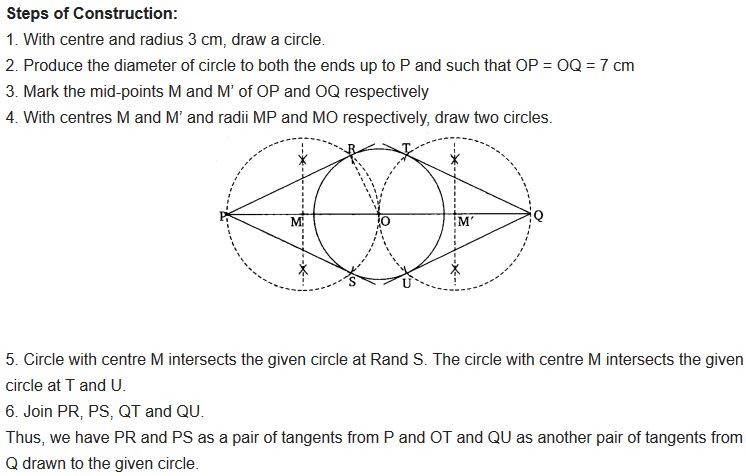
Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.
Solution:

Question 4.
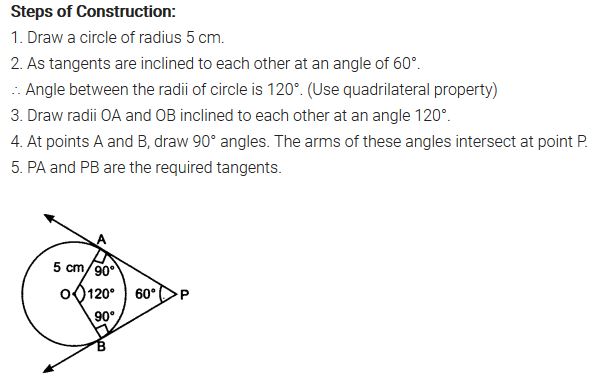
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
Solution:

Question 5.
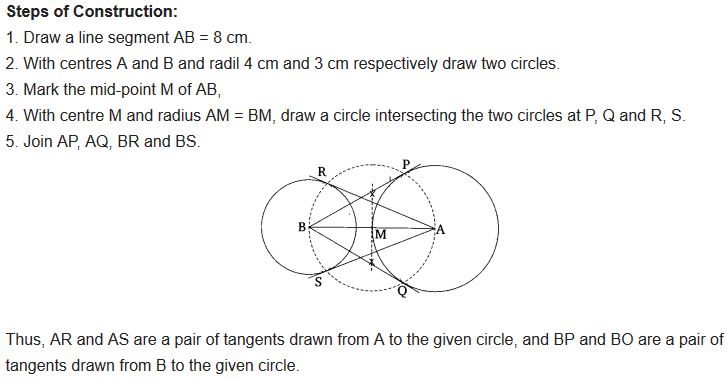
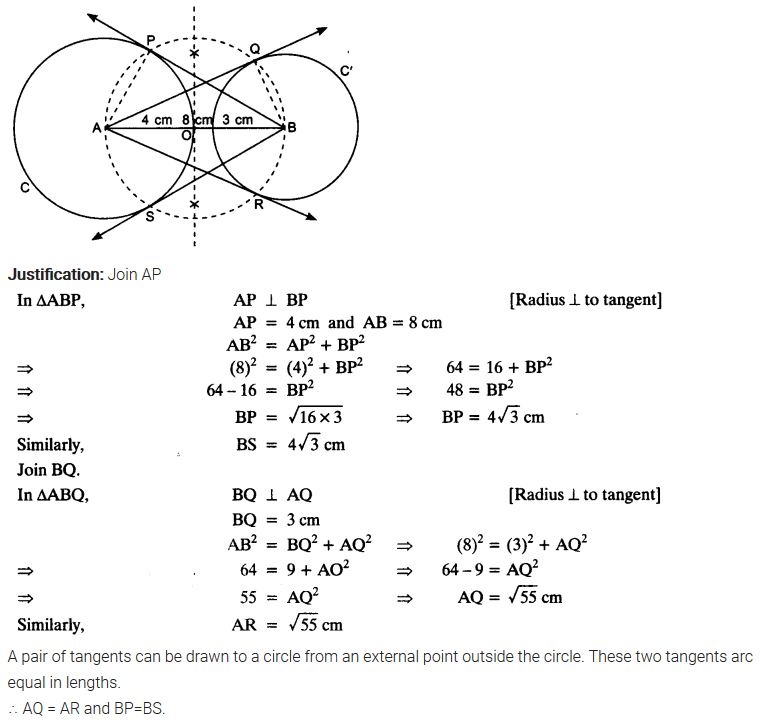
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Solution:

Question 6.
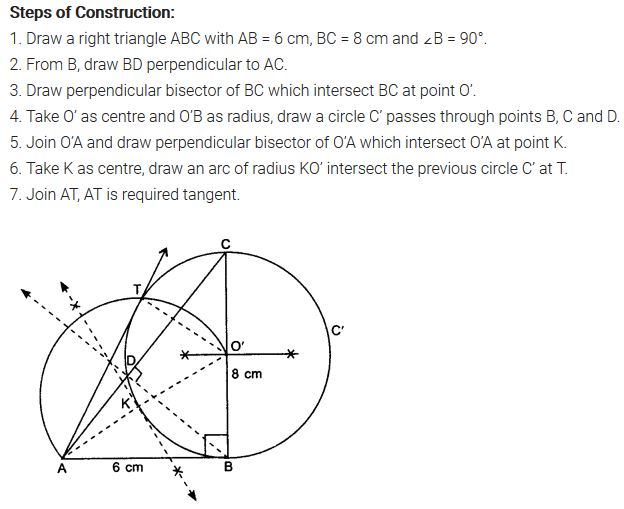
Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠B = 90°. BD is the perpendicular Burn B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Solution:

Question 7.
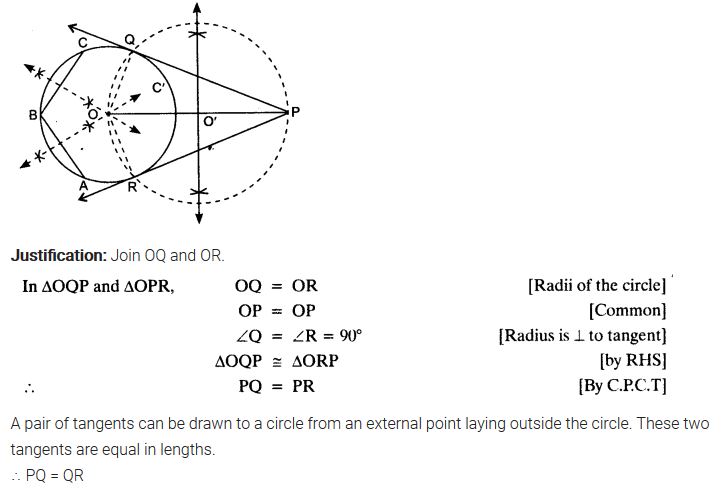
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.
Solution: