NCERT Solutions for Class 10 Maths Chapter 9 Some Applications of Trigonometry Exercise 9
NCERT Solutions For Class 10 Maths Chapter 9 Some Applications of Trigonometry Exercise 9 are prepared by specialised experienced mathematic teacher. Maths are most important subject of board and with the help of this chapter-wise NCERT solution and little practices you can get very good marks in your respective board exam. It also help students to build a foundation of upcoming class 11th and 12th. Student can also check the Important Question with solution for class 9 to class 12.
Also Check – Top 5 Best Air Cooler under 10000 in India | Best price and best features | Up to 40% Off
Class 10 Maths Chapter 9 Some Applications of Trigonometry Exercise 9 contain only 1 exercise that has 16 questions and it covered the topic how find the heights and distances of different objects using trigonometry. Check Previous chapter – NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry
Exercise 9.1
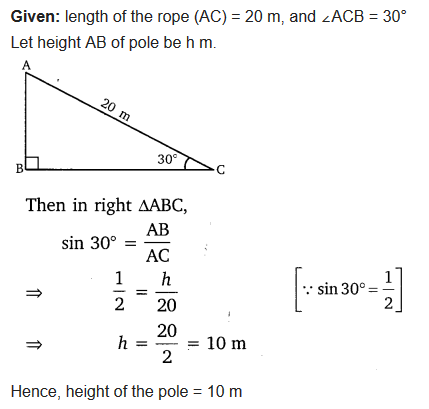
Question 1.
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.
Solution:
Question 2.
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Solution:

Question 3.
A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3 m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
Solution:

Question 4.
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30°. Find the height of the tower.
Solution:
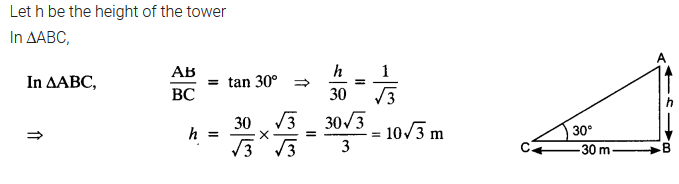
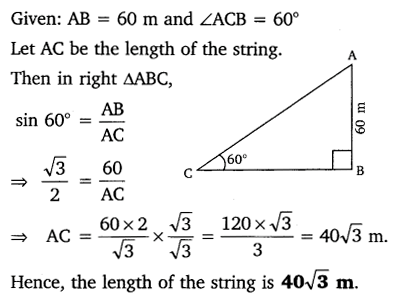
Question 5.
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Solution:
Question 6.
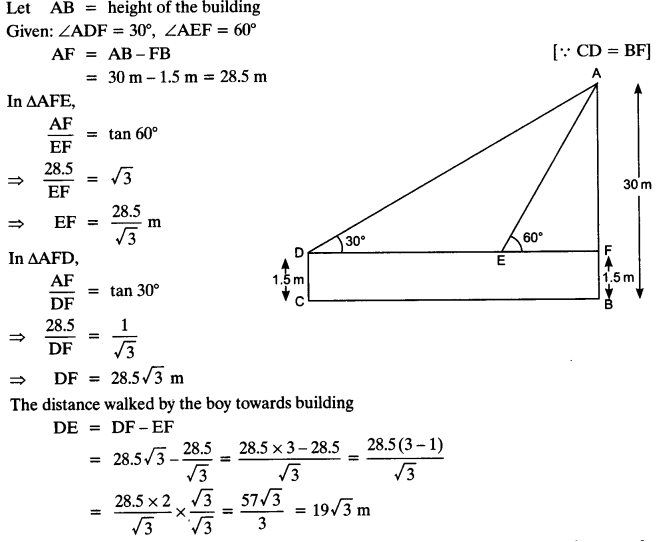
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
Solution:
Question 7.
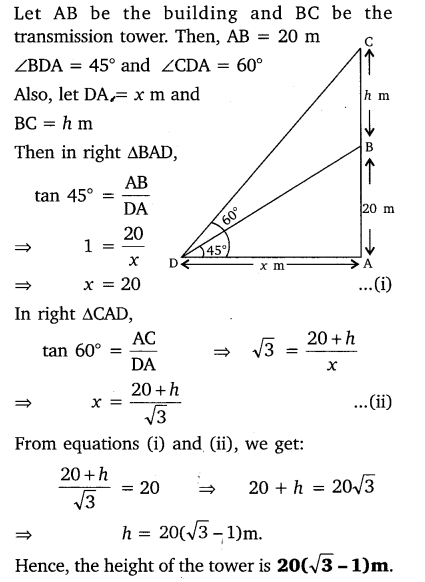
From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.
Solution:
Question 8.
A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
Solution:

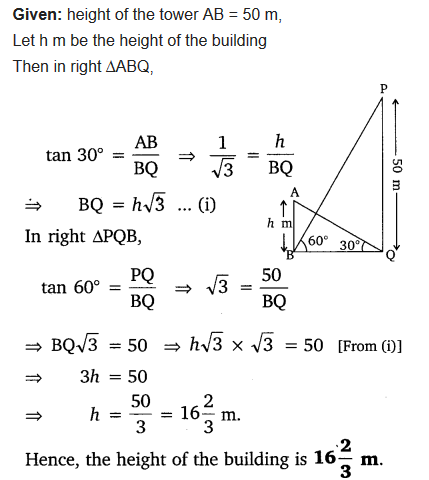
Question 9.
The angle of elevation of the top of a building from the foot of a tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
Solution:
Question 10.
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30° respectively. Find the height of the poles and the distance of the point from the poles.
Solution:

Question 11.
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30° (see the given figure). Find the height of the tower and the width of the CD and 20 m from pole AB.
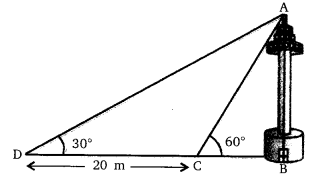
Solution:

Question 12.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Solution:
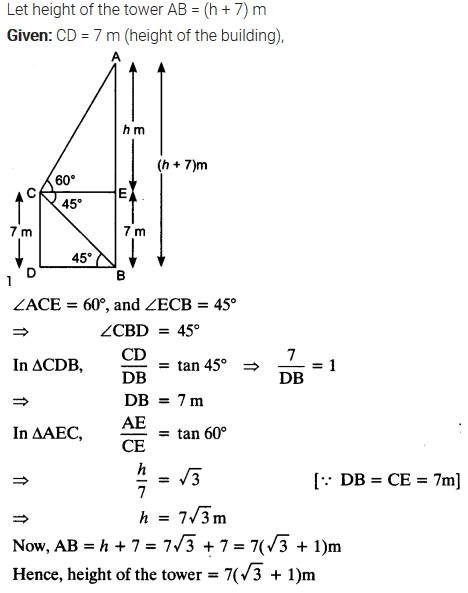
Question 13.
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Solution:
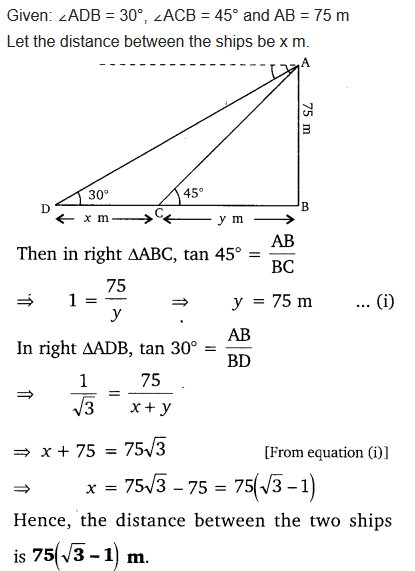
Question 14.
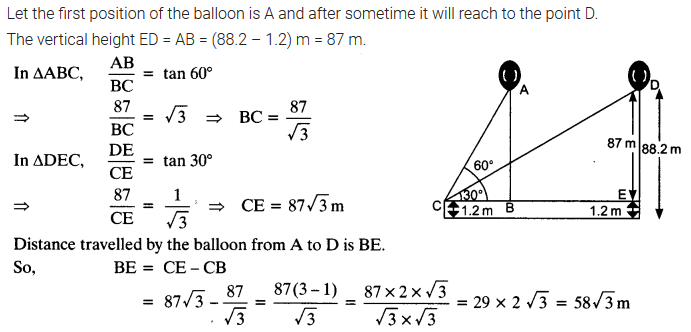
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After sometime, the angle of elevation reduces to 30° (see figure). Find the distance travelled by the balloon during the interval.
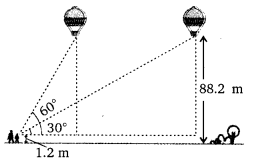
Solution:
Question 15.
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
Solution:

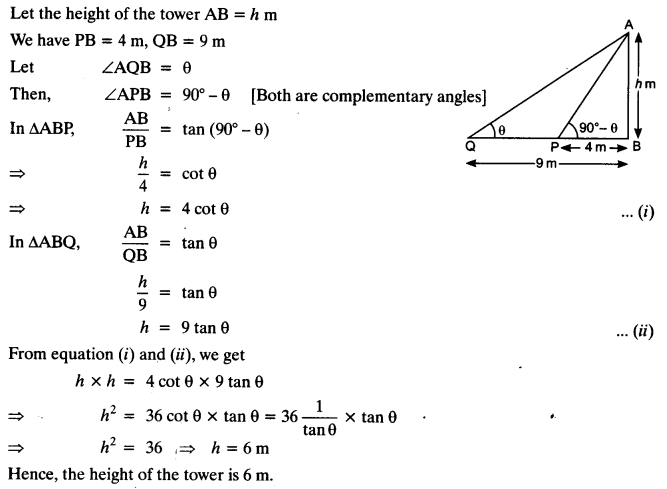
Question 16.
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Solution: