NCERT Solutions For Class 10 Maths Chapter 1 Real Numbers

Rational numbers and irrational numbers are taken together form the set of real numbers. The set of real numbers is denoted by R. Thus every real number is either a rational number or an irrational number.

Important Formulas:

Here are some of the important formulas which we used the solve problems of class 10 maths chapter 1 Real Number

HCF (p, q) × LCM (p, q) = p × q
Euclid’s division lemma: a = bq + r, 0 ≤ r < b

These are the topic that we covered in this NCERT Solutions for Class 10 Maths Chapter 1 Real Number

Euclid’s Division Algorithm
The Fundamental Theorem of Arithmetic
Revisiting Rational & Irrational Numbers
Decimal Expansions

Exercise 1.1

Question 1.

1. Use Euclid’s division algorithm to find the HCF of:
(i) $135$ and $225$ (ii) 196 and 38220 (iii) 867 and 255
Ans: We have to find the HCF of $135$ and $225$ by using Euclid’s division algorithm.
According to Euclid’s division algorithm, the HCF of any two positive integers $a$ and $b$ , where $a > b$ is found as :

First find the values of $q$ and $r$ , where $a = b q + r$ , $0 \leq r < b$ .
If $r = 0$ , the HCF is $b$ . If $r \neq 0$ , apply Euclid’s lemma to $b$ and $r$ .
Continue steps till the remainder is zero. When we get the remainder zero, divisor will be the HCF.

Let $a = 225$ and $b = 135$ .
Since, $a > b$
Using division algorithm, we get
$a = b q + r$
$\Rightarrow 225 = 135 \times 1 + 90$
Here, $\Rightarrow b = 135$ $\Rightarrow q = 1$ $\Rightarrow r = 90$
Since $r \neq 0$ , we apply the Euclid’s lemma to $b$ (new divisor) and $r$ (new remainder). We get
$\Rightarrow 135 = 90 \times 1 + 45$
Here, $\Rightarrow b = 90$ $\Rightarrow q = 1$ $\Rightarrow r = 45$
Since $r \neq 0$ , we apply the Euclid’s lemma to $b$ and $r$ . We get
$\Rightarrow 90 = 2 \times 45 + 0$
Now, we get $r = 0$ , thus we can stop at this stage.
When we get the remainder zero, divisor will be the HCF.
Therefore, the HCF of $135$ and $225$ is $45$ .

(ii) $196$ and $38220$
Ans: We have to find the HCF of $196$ and $38220$ by using Euclid’s division algorithm.
According to Euclid’s division algorithm, the HCF of any two positive integers $a$ and $b$ , where $a > b$ is found as :

First find the values of $q$ and $r$ , where $a = b q + r$ , $0 \leq r < b$ .
If $r = 0$ , the HCF is $b$ . If $r \neq 0$ , apply Euclid’s lemma to $b$ and $r$ .
Continue steps till the remainder is zero. When we get the remainder zero, divisor will be the HCF.

Let $a = 38220$ and $b = 196$ .
Since, $a > b$
Using division algorithm, we get: $a = b q + r$
$\Rightarrow 38220 = 196 \times 195 + 0$
Here, $\Rightarrow b = 196$ $\Rightarrow q = 195$ $\Rightarrow r = 0$
Since, we get $r = 0$ , thus we can stop at this stage.
When we get the remainder zero, divisor will be the HCF.
Therefore, the HCF of $196$ and $38220$ is $196$ .
(iii) $867$ and $255$
Ans: We have to find the HCF of $867$ and $255$ by using Euclid’s division algorithm.
According to Euclid’s division algorithm, the HCF of any two positive integers $a$ and $b$ , where $a > b$ is found as :

First find the values of $q$ and $r$ , where $a = b q + r$ , $0 \leq r < b$ .
If $r = 0$ , the HCF is $b$ . If $r \neq 0$ , apply Euclid’s lemma to $b$ and $r$ .
Continue steps till the remainder is zero. When we get the remainder zero, divisor will be the HCF.

Let $a = 867$ and $b = 255$ .
Since, $a > b$
Using division algorithm, we get
$a = b q + r$
$\Rightarrow 867 = 255 \times 3 + 102$
Here, $\Rightarrow b = 255$ $\Rightarrow q = 3$ $\Rightarrow r = 102$
Since $r \neq 0$ , we apply the Euclid’s lemma to $b$ (new divisor) and $r$ (new remainder). We get
$\Rightarrow 255 = 102 \times 2 + 51$
Here, $\Rightarrow b = 102$ , $\Rightarrow q = 2$ $\Rightarrow r = 51$
Since $r \neq 0$ , we apply the Euclid’s lemma to $b$ and $r$ . We get
$\Rightarrow 102 = 51 \times 2 + 0$
Now, we get $r = 0$ , thus we can stop at this stage.
When we get the remainder zero, divisor will be the HCF.
Therefore, the HCF of $867$ and $255$ is $51$ .

Question 2.
Show that any positive odd integer is of the form 6q + 1, or 6q + 3, or 6q + 5, where q is some integer.
Solution:

Let a be any positive integer and b = 6. Then, by Euclid’s algorithm, a = 6q + r, for some integer q ≥ 0, and r = 0, 1, 2, 3, 4, 5, because 0≤r<6.

Now substituting the value of r, we get,

If r = 0, then a = 6q

Similarly, for r= 1, 2, 3, 4 and 5, the value of a is 6q+1, 6q+2, 6q+3, 6q+4 and 6q+5, respectively.

If a = 6q, 6q+2, 6q+4, then a is an even number and divisible by 2. A positive integer can be either even or odd Therefore, any positive odd integer is of the form of 6q+1, 6q+3 and 6q+5, where q is some integer.

Question 3.
An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Solution:

Given,

Number of army contingent members=616

Number of army band members = 32

If the two groups have to march in the same column, we have to find out the highest common factor between the two groups. HCF(616, 32), gives the maximum number of columns in which they can march.

By Using Euclid’s algorithm to find their HCF, we get,

Since, 616>32, therefore,

616 = 32 × 19 + 8

Since, 8 ≠ 0, therefore, taking 32 as new divisor, we have,

32 = 8 × 4 + 0

Now we have got remainder as 0, therefore, HCF (616, 32) = 8.

Hence, the maximum number of columns in which they can march is 8.

Question 4.
Use Euclid’s division lemma to show that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.
Solution:
ex 1.1 class 10 maths ncert solutions

Question 5.
Use Euclid’s Division Lemma to show that the cube of any positive integer is either of the form 9m, 9m + 1 or 9m + 8.
Solution:

Let x be any positive integer and y = 3.

By Euclid’s division algorithm, then,

x = 3q+r, where q≥0 and r = 0, 1, 2, as r ≥ 0 and r < 3.

Therefore, putting the value of r, we get,

x = 3q

x = 3q + 1

x = 3q + 2

Now, by taking the cube of all the three above expressions, we get,

Case (i): When r = 0, then,

x²= (3q)³ = 27q³= 9(3q³)= 9m; where m = 3q³

Case (ii): When r = 1, then,

x³ = (3q+1)³ = (3q)³+1³+3×3q×1(3q+1) = 27q³+1+27q²+9q

Taking 9 as common factor, we get,

x³= 9(3q³+3q²+q)+1

Putting = m, we get,

Putting (3q³+3q²⁺q) = m, we get ,

x³ = 9m+1

Case (iii): When r = 2, then,

x³ = (3q+2)³= (3q)³+2³+3×3q×2(3q+2) = 27q³+54q²+36q+8

Taking 9 as common factor, we get,

x³=9(3q³+6q²+4q)+8

Putting (3q³+6q²+4q) = m, we get ,

x³ = 9m+8

Therefore, from all the three cases explained above, it is proved that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.

Exercise 1.2

Question 1.
Express each number as a product of its prime factors:
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429
Solution: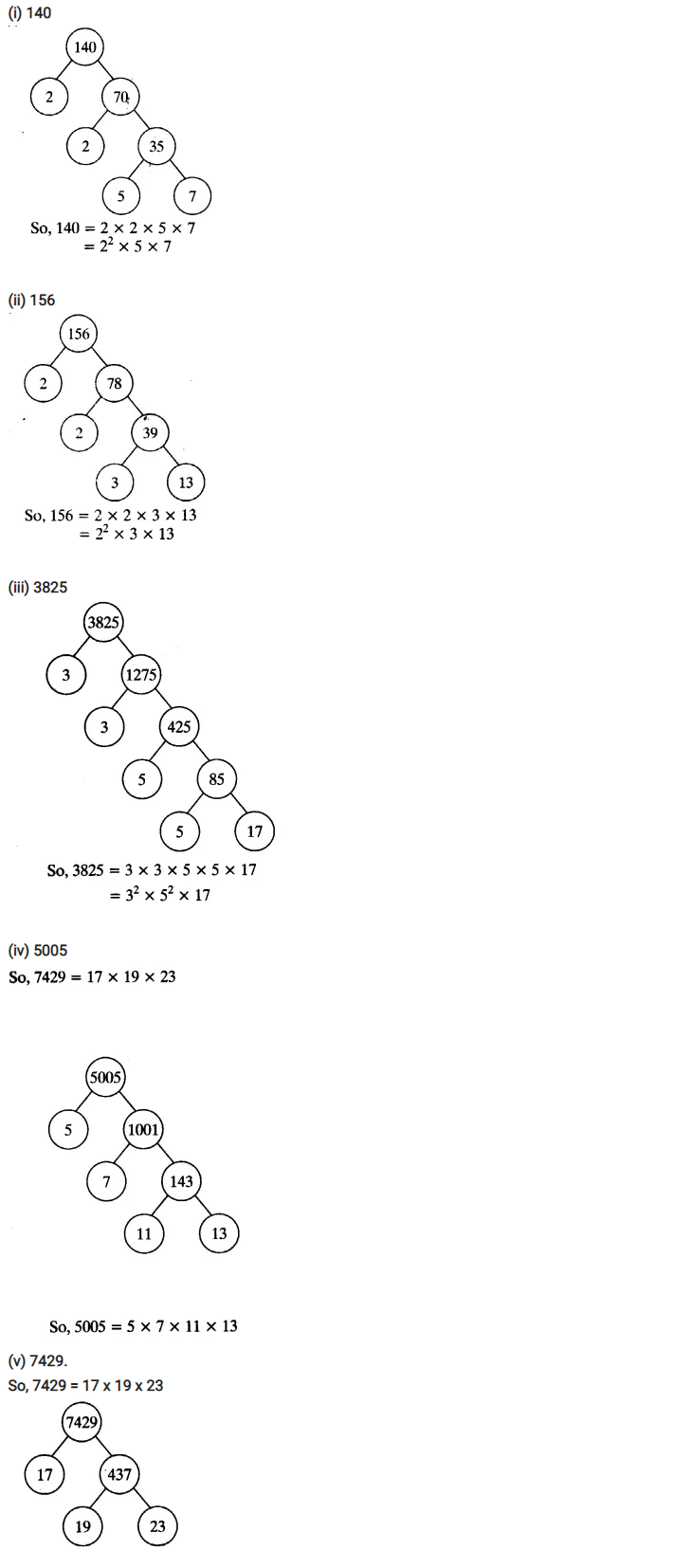
NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.2 Q1

Question 2.
Find the LCM and HCF of the following pairs of integers and verify that LCM x HCF = Product of the two numbers:
(i) 26 and 91
(ii) 510 and 92
(iii) 336 and 54
Solution:
chapter 1 class 10 maths Ex 1.2 Q2

Question 3.
Find the LCM and HCF of the following integers by applying the prime factorization method:
(i) 12, 15 and 21
(ii) 17, 23 and 29
(iii) 8, 9 and 25

Solution:

(i) 12, 15 and 21

Writing the product of prime factors for all the three numbers, we get,

12=2×2×3

15=5×3

21=7×3

Therefore,

HCF(12,15,21) = 3

LCM(12,15,21) = 2 × 2 × 3 × 5 × 7 = 420

(ii) 17, 23 and 29

Writing the product of prime factors for all the three numbers, we get,

17=17×1

23=23×1

29=29×1

Therefore,

HCF(17,23,29) = 1

LCM(17,23,29) = 17 × 23 × 29 = 11339

(iii) 8, 9 and 25

Writing the product of prime factors for all the three numbers, we get,

8=2×2×2×1

9=3×3×1

25=5×5×1

Therefore,

HCF(8,9,25)=1

LCM(8,9,25) = 2×2×2×3×3×5×5 = 1800

Question 4:
Given that HCF (306, 657) = 9, find LCM (306, 657).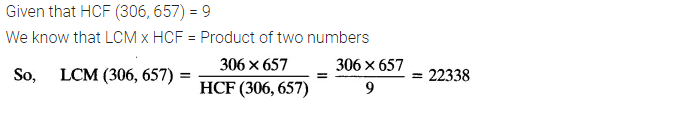
Real Numbers Class 10 Maths Chapter 1 NCERT Solutions Ex 1.2 Q4
Question 5.
Check whether 6ⁿ can end with the digit 0 for any natural number n.

Solution: If the number 6ⁿ ends with the digit zero (0), then it should be divisible by 5, as we know any number with unit place as 0 or 5 is divisible by 5.

Prime factorization of 6ⁿ = (2×3)ⁿ

Therefore, the prime factorization of 6ⁿ doesn’t contain prime number 5.

Hence, it is clear that for any natural number n, 6ⁿis not divisible by 5 and thus it proves that 6ⁿ cannot end with the digit 0 for any natural number n.

Question 6.
Explain why 7 x 11 x 13 + 13 and 7 x 6 x 5 x 4 x 3 x 2 x 1 + 5 are composite numbers.
Chapter 1 Class 10 Maths Real Numbers NCERT Solutions Ex 1.2 Q6
Question 7.
There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time and go in the same direction. After how many minutes will they meet again at the starting point?
Solution:

Sonia and Ravi move in the same direction and at the same time, the minimum time when Sonia and Ravi meet again at starting point is LCM of 18 and 12.

Therefore, LCM(18,12) = 2×3×3×2×1=36

Hence, Sonia and Ravi will meet again at the starting point after 36 minutes.

Exercise 1.3

Question 1.
Prove that √5 is irrational.
Solution:

Let us assume, that √5 is rational number.

i.e. √5 = x/y (where, x and y are co-primes)

y√5= x

Squaring both the sides, we get,

(y√5)² = x²

⇒5y² = x²……………………………….. (1)

Thus, x² is divisible by 5, so x is also divisible by 5.

Let us say, x = 5k, for some value of k and substituting the value of x in equation (1), we get,

5y² = (5k)²

⇒y² = 5k²

is divisible by 5 it means y is divisible by 5.

Clearly, x and y are not co-primes. Thus, our assumption about √5 is rational is incorrect.

Hence, √5 is an irrational number.

Question 2.
Show that 3 + √5 is irrational.
Solution:

Let us assume 3 + 2√5 is rational.

Then we can find co-prime x and y (y ≠ 0) such that 3 + 2√5 = x/y

Rearranging, we get,

ncert solutions class 10 chapter 1-1

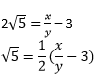
Since, x and y are integers, thus,

is a rational number.

Therefore, √5 is also a rational number. But this contradicts the fact that √5 is irrational.

So, we conclude that 3 + 2√5 is irrational.

Question 3.

Prove that the following are irrationals:

(i) 1/√2

(ii) 7√5

(iii) 6 + √2

Solution:

Exercise 1.4

Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:

(i) 13/3125 (ii) 17/8 (iii) 64/455 (iv) 15/1600 (v) 29/343 (vi) 23/(2³5²) (vii) 129/(2²5⁷7⁵) (viii) 6/15 (ix) 35/50 (x) 77/210

NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.4 Q1

Question 2.

Write down the decimal expansions of those rational numbers in Question 1 above which have terminating decimal expansions.

Solutions:

(i) 13/3125

Question 3.

The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form, p q what can you say about the prime factors of q?

(i) 43.123456789

(ii) 0.120120012000120000. . .

(i) 43.123456789

Since it has a terminating decimal expansion, it is a rational number in the form of p/q and q has factors of 2 and 5 only.

(ii) 0.120120012000120000. . .

Since, it has non-terminating and non- repeating decimal expansion, it is an irrational number.

Since it has non-terminating but repeating decimal expansion, it is a rational number in the form of p/q and q has factors other than 2 and 5.

Real Number is one of the important topics in Maths and it has a weightage of 6 marks (1×1 Marks, 2×1 Marks and 3×1 marks) in Class 10 (Unit – Number Systems) Maths first term exams. The average number of questions asked from this chapter is usually 3.

NCERT Solutions For Class 10 Maths Chapter 1 Real Numbers