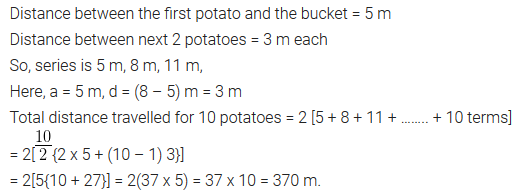NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5
NCERT Solutions For Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5 are prepared by specialised experienced mathematic teacher. Maths are most important subject of board and with the help of this chapter-wise NCERT solution and little practices you can get very good marks in your respective board exam. It also help to build a foundation for topics that will be covered in the upcoming 11th and 12th. Student can also check the Important Question with solution for class 9 to class 12.
Also Check – Best laptop under 30000 for student
Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5 chapter contain total 4 exercise and it covered the topic form of AP, finding the first term and difference of an AP, finding the nth term of an AP, sum of first n terms of an AP. Check Previous chapter –NCERT Solutions For Class 10 Maths Chapter 4 Quadratic Equations
Important Formulas:
- nth term of AP: an = a + (n – 1) d
- Sum of n terms: S = n/2[2a + (n – 1) d]
Exercise 5.1
Question 1.
In which of the following situations, does the list of numbers involved make an arithmetic progression and why?
(i) The taxi fare after each km when the fare is ₹ 15 for the first km and ₹ 8 for each additional km.
(ii) The amount of air present in a cylinder when a vacuum pump removes 14 of the air remaining in the cylinder at a time.
(iii) The cost of digging a well after every meter of digging, when it costs ₹ 150 for the first meter and rises by ₹ 50 for each subsequent meter.
(iv) The amount of money in the account every year, when ₹ 10000 is deposited at compound interest at 8% per annum.
Solution:
(i) We can write the given condition as;
Taxi fare for 1 km = 15
Taxi fare for first 2 kms = 15+8 = 23
Taxi fare for first 3 kms = 23+8 = 31
Taxi fare for first 4 kms = 31+8 = 39
And so on……
Thus, 15, 23, 31, 39 … forms an A.P. because every next term is 8 more than the preceding term.
(ii)Solution:
Let the volume of air in a cylinder, initially, be V litres.
In each stroke, the vacuum pump removes 1/4th of air remaining in the cylinder at a time. Or we can say, after every stroke, 1-1/4 = 3/4th part of air will remain.
Therefore, volumes will be V, 3V/4 , (3V/4)2 , (3V/4)3…and so on
Clearly, we can see here, the adjacent terms of this series do not have the common difference between them. Therefore, this series is not an A.P.
(iii) Solution:
We can write the given condition as;
Cost of digging a well for first metre = Rs.150
Cost of digging a well for first 2 metres = Rs.150+50 = Rs.200
Cost of digging a well for first 3 metres = Rs.200+50 = Rs.250
Cost of digging a well for first 4 metres =Rs.250+50 = Rs.300
And so on..
Clearly, 150, 200, 250, 300 … forms an A.P. with a common difference of 50 between each term.
(iv) Solution:
We know that if Rs. P is deposited at r% compound interest per annum for n years, the amount of money will be:
P(1+r/100)n
Therefore, after each year, the amount of money will be;
10000(1+8/100), 10000(1+8/100)2, 10000(1+8/100)3……
Clearly, the terms of this series do not have the common difference between them. Therefore, this is not an A.P.
Question 2.
Write first four terms of the AP, when the first term a and the common difference d are given as follows:
(i) a = 10, d = 10
(ii) a = -2, d = 0
(iii) a = 4, d = -3
(iv) a = -1, d = 12
(v) a = -1.25, d = -0.25
Solution:

(iv) a = – 1, d = 1/2
Let us consider, the Arithmetic Progression series be a1, a2, a3, a4, a5 …
a2 = a1+d = -1+1/2 = -1/2
a3 = a2+d = -1/2+1/2 = 0
a4 = a3+d = 0+1/2 = 1/2
Thus, the A.P. series will be-1, -1/2, 0, 1/2
And First four terms of this A.P. will be -1, -1/2, 0 and 1/2.
(v) a = – 1.25, d = – 0.25
Let us consider, the Arithmetic Progression series be a1, a2, a3, a4, a5 …
a1 = a = – 1.25
a2 = a1 + d = – 1.25-0.25 = – 1.50
a3 = a2 + d = – 1.50-0.25 = – 1.75
a4 = a3 + d = – 1.75-0.25 = – 2.00
Therefore, the A.P series will be 1.25, – 1.50, – 1.75, – 2.00 ……..
And first four terms of this A.P. will be – 1.25, – 1.50, – 1.75 and – 2.00.
Question 3.
For the following APs, write the first term and the common difference:
(i) 3, 1, – 1, – 3 …
(ii) -5, – 1, 3, 7 …
(iii) 1/3, 5/3, 9/3, 13/3 ….
(iv) 0.6, 1.7, 2.8, 3.9 …
Solution:
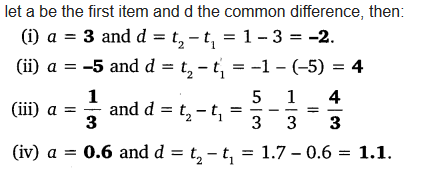
Question 4.
Which of the following are APs ? If they form an AP, find the common difference d and write three more terms.
(i) 2, 4, 8, 16 …
(ii) 2, 5/2, 3, 7/2 ….
(iii) -1.2, -3.2, -5.2, -7.2 …
(iv) -10, – 6, – 2, 2 …
(v) 3, 3 + √2, 3 + 2√2, 3 + 3√2
(vi) 0.2, 0.22, 0.222, 0.2222 ….
(vii) 0, – 4, – 8, – 12 …
(viii) -1/2, -1/2, -1/2, -1/2 ….
(ix) 1, 3, 9, 27 …
(x) a, 2a, 3a, 4a …
(xi) a, a2, a3, a4 …
(xii) √2, √8, √18, √32 …
(xiii) √3, √6, √9, √12 …
(xiv) 12, 32, 52, 72 …
(xv) 12, 52, 72, 73 …
Solution:


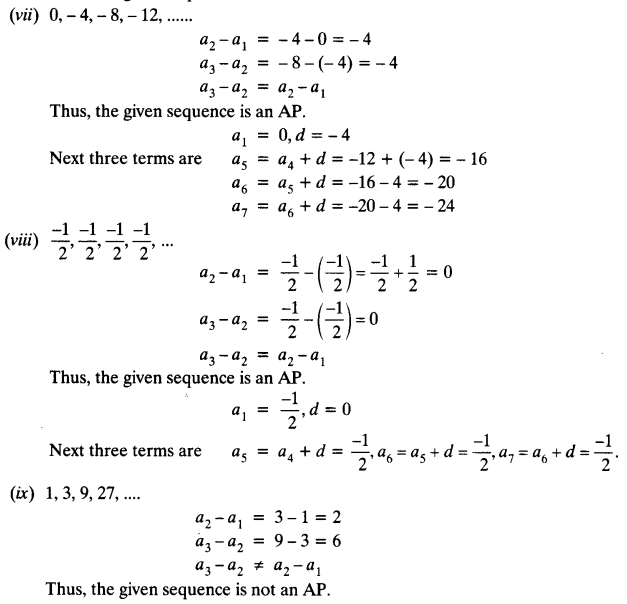
Exercise 5.2
Question 1.
Fill in the blanks in the following table, given that a is the first term, d the common difference and the nth term of the AP:

Solutions:
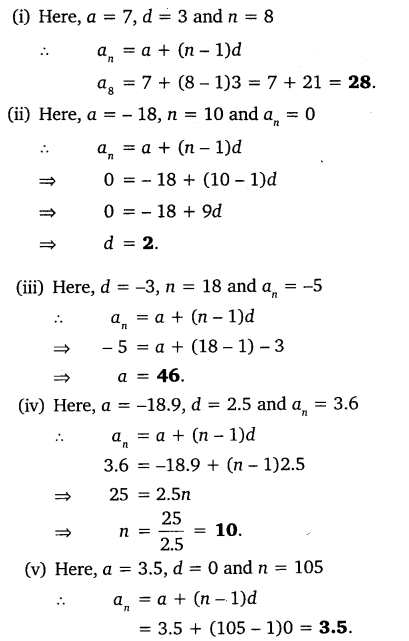
Question 2.
Choose the correct choice in the following and justify:
(i) 30th term of the A.P: 10,7, 4, …, is
(A) 97
(B) 77
(C) −77
(D) −87
(ii) 11th term of the A.P. -3, -1/2, ,2 …. is
(A) 28
(B) 22
(C) – 38
(D)![]()
Solution:

Question 3.
In the following APs, find the missing terms in the boxes:
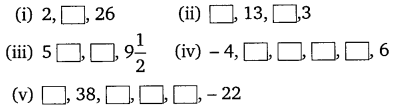
Solution:
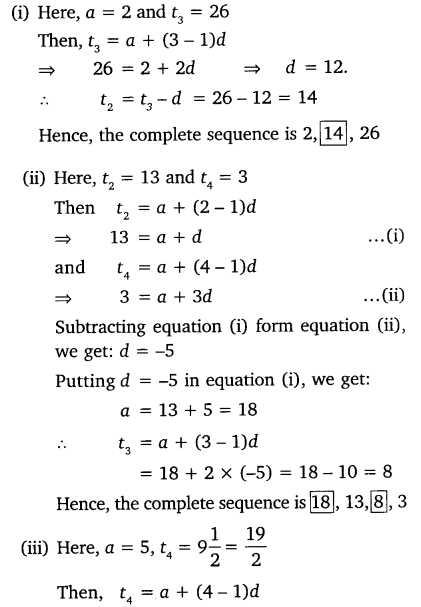


Question 4. Which term of the A.P. 3, 8, 13, 18, … is 78?
Solutions:
Given the A.P. series as3, 8, 13, 18, …
First term, a = 3
Common difference, d = a2 − a1 = 8 − 3 = 5
Let the nth term of given A.P. be 78. Now as we know,
an = a+(n−1)d
Therefore,
78 = 3+(n −1)5
75 = (n−1)5
(n−1) = 15
n = 16
Hence, 16th term of this A.P. is 78.
Question 5. Find the number of terms in each of the following A.P.
(i) 7, 13, 19, …, 205
![]()
Solutions:
(i) Given, 7, 13, 19, …, 205 is the A.P
Therefore
First term, a = 7
Common difference, d = a2 − a1 = 13 − 7 = 6
Let there are n terms in this A.P.
an = 205
As we know, for an A.P.,
an = a + (n − 1) d
Therefore, 205 = 7 + (n − 1) 6
198 = (n − 1) 6
33 = (n − 1)
n = 34
Therefore, this given series has 34 terms in it.
![]()
First term, a = 18
Common difference, d = a2-a1 =
![]()
d = (31-36)/2 = -5/2
Let there are n terms in this A.P.
an = -47
As we know, for an A.P.,
an = a+(n−1)d
-47 = 18+(n-1)(-5/2)
-47-18 = (n-1)(-5/2)
-65 = (n-1)(-5/2)
(n-1) = -130/-5
(n-1) = 26
n = 27
Therefore, this given A.P. has 27 terms in it.
Question 6.
Check, whether -150 is a term of the AP: 11, 8, 5, 2, ….
Solution:

Question 7.
Find the 31st term of an AP whose 11th term is 38 and the 16th term is 73.
Solution:
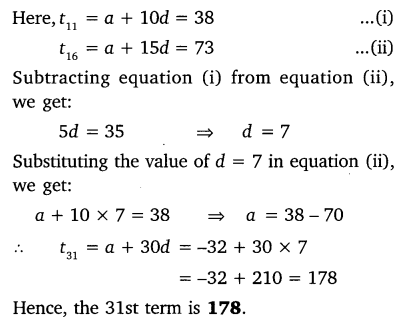
Question 8.
An AP consists of 50 terms of which 3rd term is 12 and the last term is 106. Find the 29th term.
Solution:
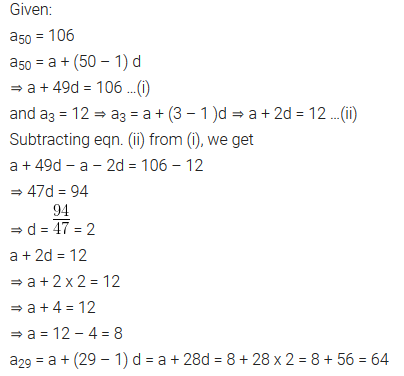
Question 9.
If the 3rd and the 9th term of an AP are 4 and -8 respectively, which term of this AP is zero?
Solution:

Question 10.
The 17th term of an AP exceeds its 10th term by 7. Find the common difference.
Solution:
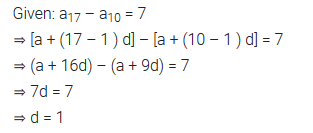
Question 11.
Which term of the AP: 3, 15, 27, 39, … will be 132 more than its 54th term?
Solution:
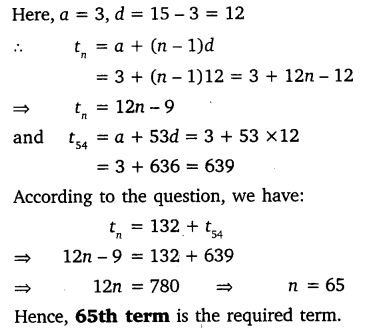
Question 12.
Two APs have the same common difference. The difference between their 100th terms is 100, what is the difference between their 1000th terms?
Solution:

Question 13.
How many three-digit numbers are divisible by 7?
Solution:
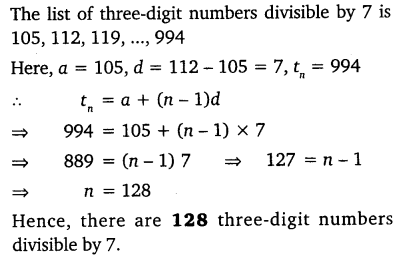
Question 14.
How many multiples of 4 lie between 10 and 250?
Solution:
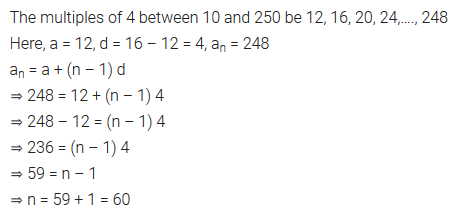
Question 15.
For what value of n, the nth term of two APs: 63, 65, 61,… and 3, 10, 17,… are equal?
Solution:

Question 16.
Determine the AP whose 3rd term is 16 and 7th term exceeds the 5th term by 12.
Solution:
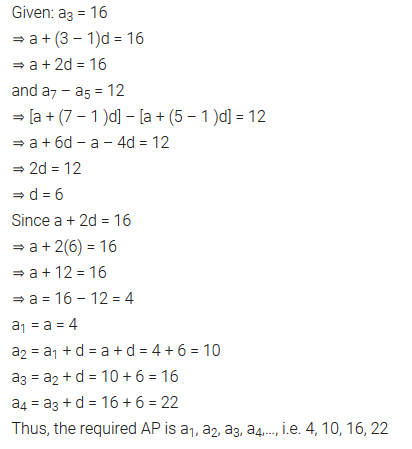
Question 17.
Find the 20th term from the last term of the AP: 3, 8, 13, …, 253.
Solution:

Question 18.
The sum of the 4th and 8th terms of an AP is 24 and the sum of the 6th and 10th terms is 44. Find the first three terms of the AP.
Solution:
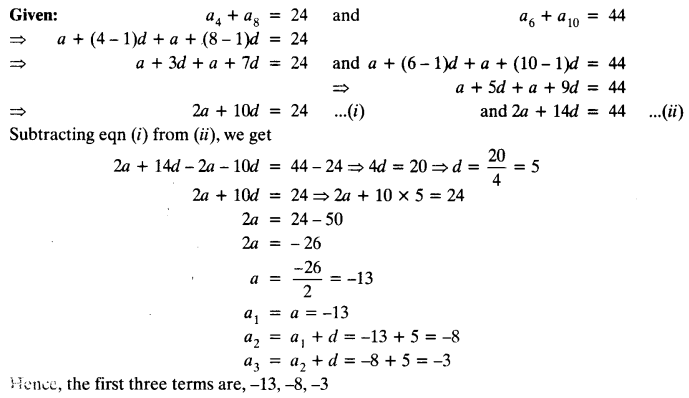
Question 19.
Subba Rao started work in 1995 at an annual salary of ₹ 5000 and received an increment of ₹ 200 each year. In which year did his income reach ₹ 7000 ?
Solution:

Question 20.
Ramkali saved ₹ 5 in the first week of a year and then increased her weekly saving by ₹ 1.75. If in the nth week, her weekly saving become ₹ 20.75, find n.
Solution:
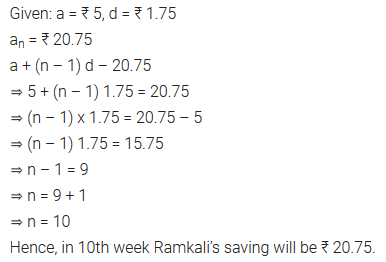
Exercise 5.3
Question 1.
Find the sum of the following APs:
(i) 2, 7, 12 ,…., to 10 terms.
(ii) − 37, − 33, − 29 ,…, to 12 terms
(iii) 0.6, 1.7, 2.8 ,…….., to 100 terms
(iv) 1/15, 1/12, 1/10, …… , to 11 terms
Solutions:
(i) Given, 2, 7, 12 ,…, to 10 terms
For this A.P.,
first term, a = 2
And common difference, d = a2 − a1 = 7−2 = 5
n = 10
We know that, the formula for sum of nth term in AP series is,
Sn = n/2 [2a +(n-1)d]
S10 = 10/2 [2(2)+(10 -1)×5]
= 5[4+(9)×(5)]
= 5 × 49 = 245
(ii) Given, −37, −33, −29 ,…, to 12 terms
For this A.P.,
first term, a = −37
And common difference, d = a2− a1
d= (−33)−(−37)
= − 33 + 37 = 4
n = 12
We know that, the formula for sum of nth term in AP series is,
Sn = n/2 [2a+(n-1)d]
S12 = 12/2 [2(-37)+(12-1)×4]
= 6[-74+11×4]
= 6[-74+44]
= 6(-30) = -180
(iii) Given, 0.6, 1.7, 2.8 ,…, to 100 terms
For this A.P.,
first term, a = 0.6
Common difference, d = a2 − a1 = 1.7 − 0.6 = 1.1
n = 100
We know that, the formula for sum of nth term in AP series is,
Sn = n/2[2a +(n-1)d]
S12 = 50/2 [1.2+(99)×1.1]
= 50[1.2+108.9]
= 50[110.1]
= 5505
(iv) Given, 1/15, 1/12, 1/10, …… , to 11 terms
For this A.P.,
First term, a = 1/5
Common difference, d = a2 –a1 = (1/12)-(1/5) = 1/60
And number of terms n = 11
We know that, the formula for sum of nth term in AP series is,
Sn = n/2 [2a + (n – 1) d]

= 11/2(2/15 + 10/60)
= 11/2 (9/30)
= 33/20
Question 2.
Find the sums given below:
![]()
(ii) 34 + 32 + 30 + ……….. + 10
(iii) − 5 + (− 8) + (− 11) + ………… + (− 230)
Solutions:
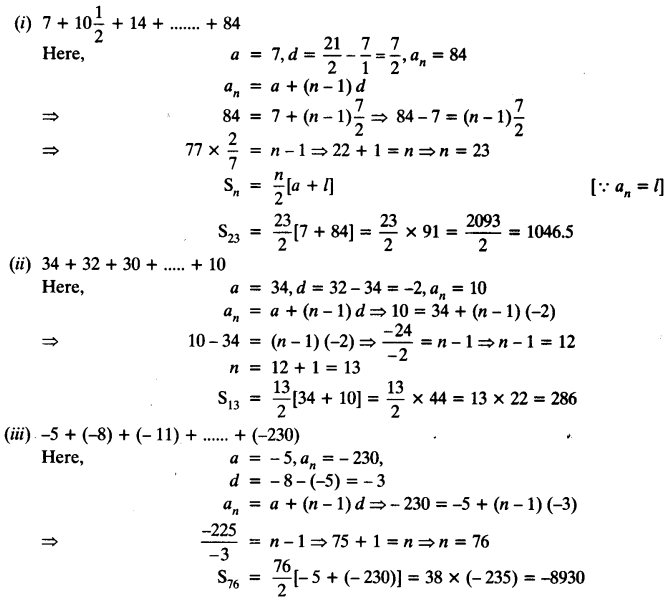
Question 3.
In an AP:
(i) given a = 5, d = 3, an = 50, find n and Sn.
(ii) given a = 7, a13 = 35, find d and S13.
(iii) given a12 = 37, d = 3, find a and S12.
(iv) given a3 = -15, S10 = 125, find d and a10.
(v) given d = 5, S9 = 75, find a and a9.
(vi) given a = 2, d = 8, Sn = 90, find n and an.
(vii) given a = 8, an = 62, Sn = 210, find n and d.
(viii) given an = 4, d = 2, Sn = -14, find n and a.
(ix) given a = 3, n = 8, S = 192, find d.
(x) given l = 28, S = 144, and there are total 9 terms. Find a.
Solution:
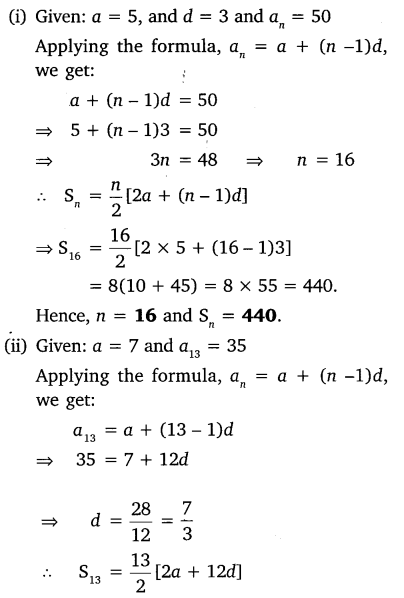

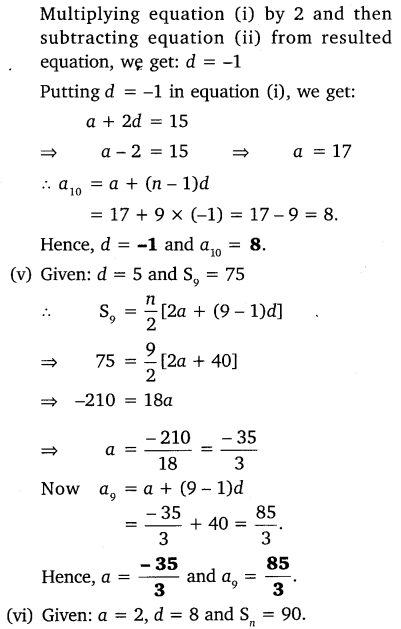

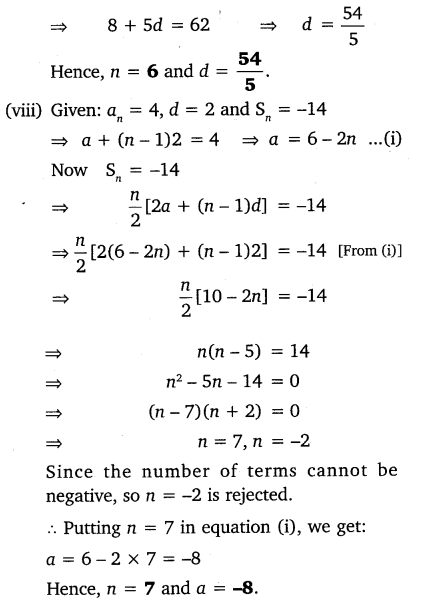
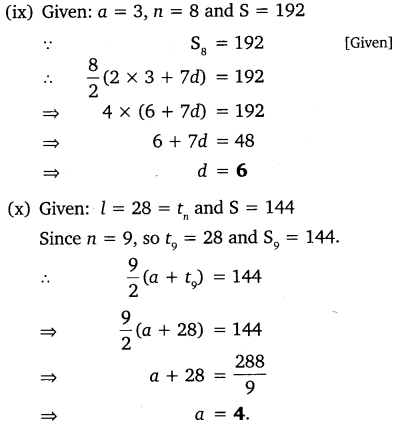
Question 4.
How many terms of AP: 9, 17, 25, … must be taken to give a sum of 636?
Solution:
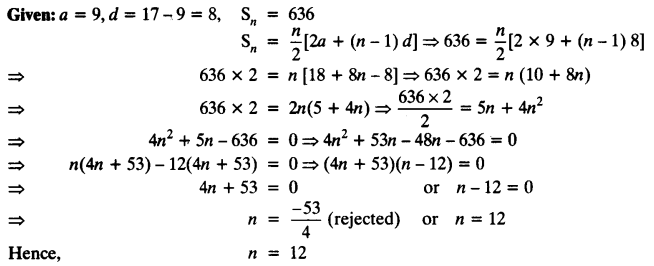
Question 5.
The first term of an AP is 5, the last term is 45 and the sum is 400. Find the number of terms and the common difference.
Solution:
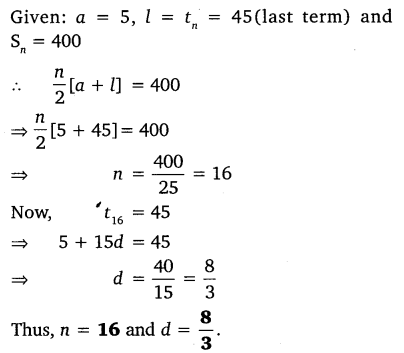
Question 6.
The first and the last terms of an AP are 17 and 350 respectively. If the common difference is 9, how many terms are there and what is their sum?
Solution:
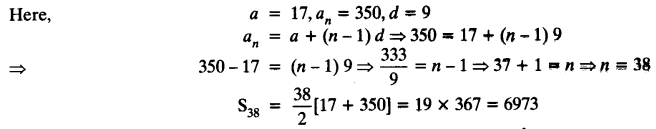
Question 7.
Find the sum of first 22 terms of an AP in which d = 7 and 22nd term is 149.
Solution:
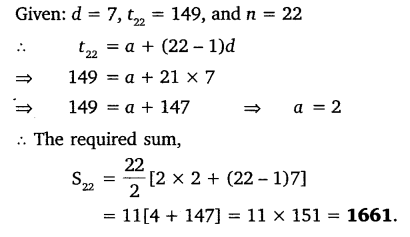
Question 8.
Find the sum of first 51 terms of an AP whose second and third terms are 14 and 18 respectively.
Solution:
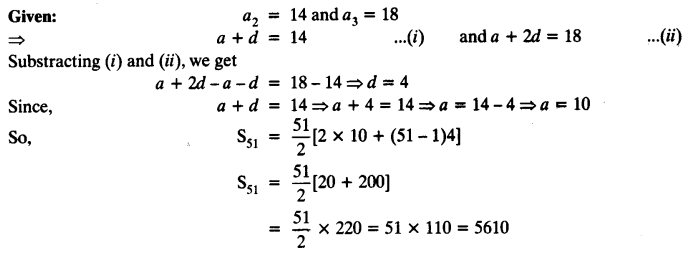
Question 9.
If the sum of first 7 terms of an AP is 49 and that of 17 terms is 289, find the sum of first n terms.
Solution:
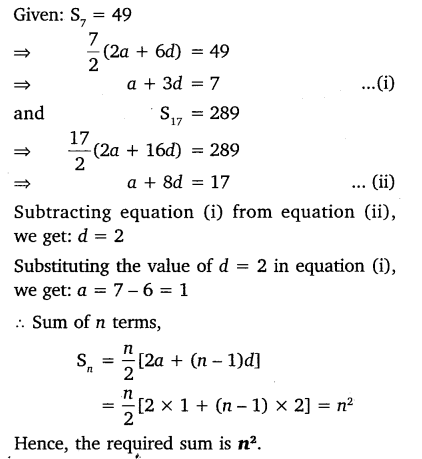
Question 10.
Show that a1, a2, ……. an,…… form an AP where an is defined as below:
(i) an = 3 + 4n
(ii) an = 9 – 5n
Also find the sum of the first 15 terms in each case.
Solution:

Question 11.
If the sum of the first n terms of an AP is 4n – n2, what is the first term (that is S1)? What is the sum of first two terms? What is the second term? Similarly, find the 3rd, the 10th and the nth terms.
Solution:

Question 12.
Find the sum of the first 40 positive integers divisible by 6.
Solution:
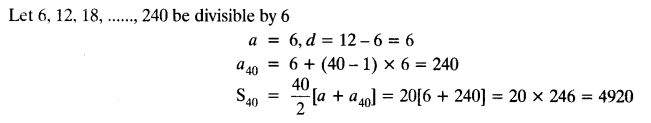
Question 13.
Find the sum of the first 15 multiples of 8.
Solution:
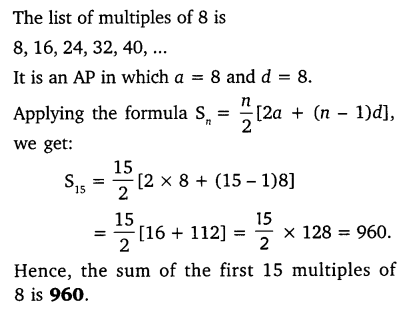
Question 14.
Find the sum of the odd numbers between 0 and 50.
Solution:
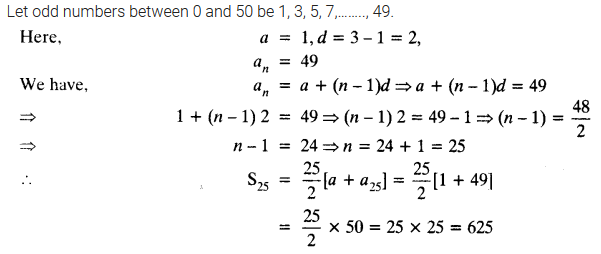
Question 15.
A contract on construction job specifies a penalty for delay of completion beyond a certain date as follows:
₹ 200 for the first day, ₹ 250 for the second day, ₹ 300 for the third day, etc. the penalty for each succeeding day being ₹ 50 more than for the preceding day. How much money the contractor has to pay as penalty, if he has delayed the work by 30 days?
Solution:

Question 16.
A sum of ₹ 700 is to be used to give seven cash prizes to students of a school for their overall academic performance. If each prize is ₹ 20 less than its preceding prize, find the value of each of the prizes.
Solution:
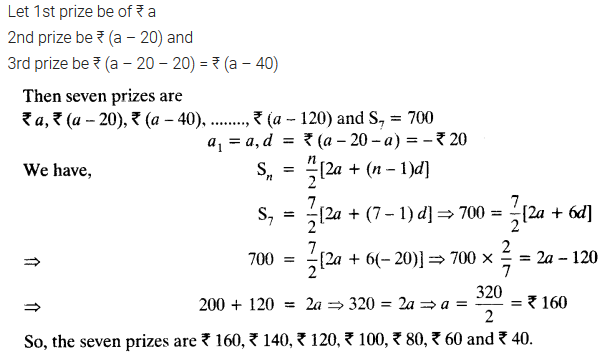
Question 17.
In a school, students thought of planting trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be the same as the class, in which they are studying, eg. a section of Class I will plant 1 tree, a section of Class II will plant 2 trees and so on till Class XII. There are three sections of each class. How many trees will be planted by the students?
Solution:

Question 18.
A spiral is made up of successive semicircles, with centres alternately at A and B, starting with centre at A, of radii 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm,… as shown in figure. What is the total length of such a spiral made up of thirteen consecutive semicircles?
(Take π = 227)
[Hint: Length of successive semicircles is l1, l2, l3, l4, … with centres at A, B, respectively.]
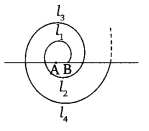
Solution:
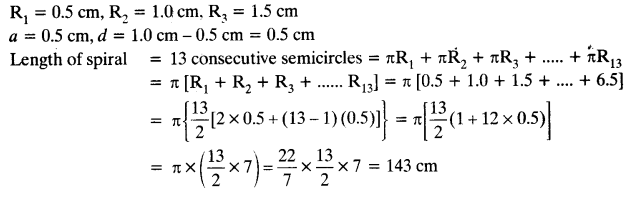
Question 19.
200 logs are stacked in the following manner 20 logs in the bottom row, 19 in the next row, 18 in the row next to it and so on (see Figure). In how many rows are the 200 logs placed and how many logs are in the top row?
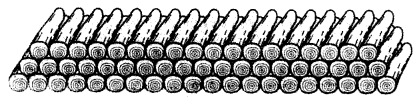
Solution:
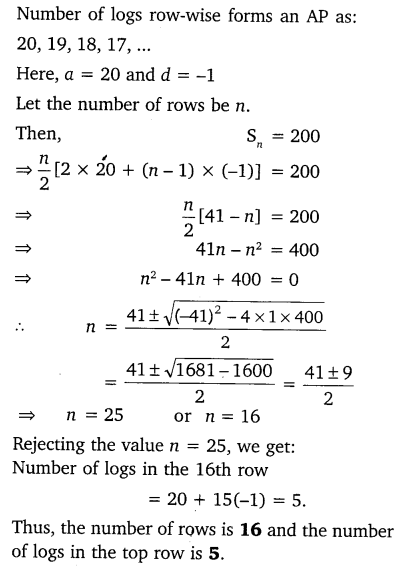
Question 20.
In a potato race, a bucket is placed at the starting point, which is 5 m from the first potato, and the other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line

A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are in the bucket. What is the total distance the competitor has to run?
Solution: